Particle physics - Germany
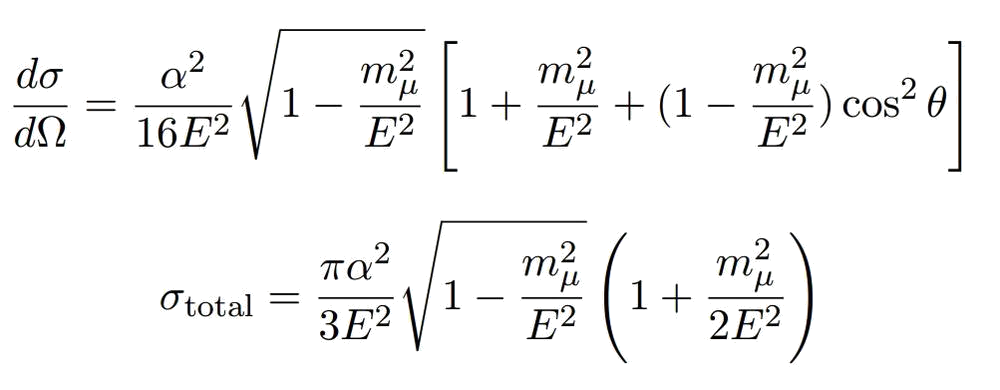
I was in charge of example classes for advanced particle physics lecture in Karl Jakobs group, at Freiburg University (Germany). This lecture basically covers the genesis of the Standard Model, the experimental validations and a presentation of phenonena beyond the Standard Model. Also, the formalism to link a theory to observables is discussed in different context (collider physics, neutrino oscillation, low energy limits..)
The exercises that were given to the students started with mostly formalism and slowly turned into pratical work using collision simulations. Students had to analyze them with ROOT in order to link collisions to the underlying fundamental theory. Below are listed the topics which were covered in the exercises.
1. Relativistic Kinematics and Neutrino Oscillation
This sheet targets the basics of special relativity, namely time "dilation" and distance "contraction" as well as energy thresholds in different type of collisions. It also contains a first description of neutrino oscillations (two flavours scheme).
2. Realistic Neutrino Oscillations
This sheet gives a more realistic description of neutrino oscillations with three flavours, including the relevant order of magnitudes. A first description of the effect of matter on oscillations is also introduced using an effective hamiltonian (Mikheyev–Smirnov–Wolfenstein effect).
3. Description of spin-1/2 Particles: Dirac Field
This sheet presents the dynamic of the elementary block of matter, the spin-1/2 particles. First the free solution of the Dirac equation are derived, then few relativistic invariants are build from Dirac bi-spinnors. The low energy limit of Dirac equation is studied to demonstrate the famous "g=2" equation.
4. Elementary Processes: Transition Amplitudes and Cross Sections
This sheet give the first computation of a cross section from first principles. The relation between transition amplitude and cross section is first derived, then the transition amplitude between |ee> and |μμ> states is computed using perturbative developpement and Feynman diagrams.
5. Structure of Amplitudes - Experimental Test of QED
This sheet aims to give a feeling of how each typical amplitude behaves in term of physical observables. The Mandlestam variables are introduced and the corresponding ampludes are scrutinized, in particular their dependance with incoming/outcoming particle directions. Measurement of cross-section for different energies are analyzed to extract the mass of the tau lepton.
6. Introduction to Simulation and Study of Few QCD Processes
The goal of this session is to be able to run an event generator - for instance pythia - and analyze the collision with ROOT. As an application, the study of two elementary QCD processes during proton-proton collision is proposed (energy andcharge conservation, angular distributions ...)
7. Experimental Signature of Quarks and Gluons
This sheet is meant to introduce the concept of particle jet, obtained in QCD when a coloured particle is produced. The fundamental property of QCD involved is discussed, then a simulation with pythia is studied.
8. Phenomenology and Experimental Aspects of the Top Quark
The basics of the top quark is detailed, and the consequences in term of experimental strategy are also discussed in this sheet. As an illustration a simulation of top-antitop production is analyzed. In particular, a method of the top mass reconstruction is proposed, based on semi-leptonic decay of the top-antitop pair.
9. Few Aspects of the Electroweak Interaction
In this sheet, the consequences of the V-A structure of the electroweak interaction are explored (from meson decays to helicity/direction correlations). Then, the muon decay is formally strudied and formulas are related to experimental data to extract some of the fundamental parameters of the theory.
10. Forward-Backward Asymmetry in the Electroweak Interaction
This sheet presents one of the most specific signature of the structure of the electroweak sector, the forward-backward asymmetry for neutral current interactions. After studing the analytical formulaes, a sample of simulated Z production is used to extract the value of the Weinberg angle.
11. Electroweak Symmetry Breaking and Higgs Mechanism
The last sheet concludes the lecture by the corner stone of the Standard Model, the sponanous breakink of the electroweak gauge invariance. The Higgs mechanism is briefly discussed, and the physical states for gauge bosons (mass eigenstates) are derived.
General physics
Elementary mechanics - Germany
I gave example classes in first year of universtiy. This was an interesting experience especially because of the difference between french and german system. The subjects of these example classes actually covered much more than what it's done in first year in a french university. However, the approach was more qualitative than computational allowing to touch several physics topics. For example, sound propagation, fluid statics or coupled oscillators were quickly discussed (while this would be done in L2 or L3 in France). More information can be found on this supporting material

Classical physics and sligthly beyond - France "Math Spé"
In the french system, there are preparatory classes for competitive exam allowing to enter in one of the french "grande écoles". In these classes, there are weekly oral examinations to better prepare the final exam, covering the whole program, ie basically general physics up the 18th century. I gave these examinations for one year at Lycée Saint-Louis, covering the topics described below.
All ressouces are available here but only french is available. Quality of the document is debatable - it was one of the first document I wrote in LaTeX.
1. Thermodynamics
This part is dedicated to classical thermodynamics with a light touch of statistical physics. A dozen of exercises cover irreversible processes, kinetic theory of gaz, black body physics, or even thermodynamics applied to chimcal reactions.
2. Mechanics
In this section, relatively advanced problems of mechanics are discussed, often connected with other physics areas. As few examples, one can mention a description of atoms, the Einstein and Haas experiment or the discussion about inhertial and gravitational mass - which is at the center of modern physics!
3. Physics of waves
The basic (but useful) transition between a collection of N harmonic oscillators and waves is derived. Then several broad phenomena are stuided, such as guitar string spectra and intital conditions, radiation pressues or the interesting parallel between the Meissner effect and skin effect.
4. Electromagnetism
Of course, the full edifice of Maxwell equations are deeply studied in this section. Essentially, many simple phenomena are described from first princples and the news aspect of electromagnetic field (induction, energy, impulsion) are analyzed a bit more in details. The way the electroscope works is presented and it's application in cosmic ray discovery!
5. Optics
Difficult to resist of presenting a classical approach of the atom, the light produced by the electron "turning" around and the relation between spectral properties of the light and the atom structure! Maxwell equations are also used to describe light propagation in a medium: refractive index from first principle!
Mathematics for physics - France
When I was doing my PhD, I got in charge of an entire lecture: introduction to mathematics for physics. The context was a bit special since it was for continuing education of technicians in order to become engineer. I had to design from scratch an full progression starting from high school mathematics toward common tools used in physics such as vectorial calculus or functions with several variables. It was really interesting to make concepts clear with a minimal - but necessary - touch of formalism, while keeping the operational know-how of mathematics applied to basic situations. People following the training came from several areas with multiple scientific backgrounds. This lecture was done in Polytech Paris Sud engineer school, and the only available material is a french blog I wrote back in 2009!
0. Why the mathematics in physics?
Such a vast and deep question ... In this pre-introduction chapter, the goal is just to explain the place of the mathematics in the description of Nature. Prediction, make concepts effective via formalism, quatitative analysis, precisions ... In two words: no mathematics, no understanding of Nature! Why? If only somone knew...
1. Basics of analysis, algebra and geometry
The basic mathematics tool box of high school student is presented here, to make sure everyone starts with the same level. Usual functions, simple algebra and geometry are reviewed.
2. Hyperbolic functions
This chapter simply introduce even and odd component of exponantial function. Applications in physics in cases where symmetries are explicit through boudary conditions. The Ising model solution, given by hyperbolic tangente, is also discussed in a new context: how a decision is made in a company!
3. Taylor series
This notion is obviously needed in many contexts, such as undetermined limits or resolution of non-linear equation in a given limit. The fundamental idea is presented, and the main technics to compute taylor series are discussed. Key examples are shown, such as the classical - but so fundamental - hamonic oscillator.
4. Integrals
Integrals are introduced as contious sum of numbers (Riemann sum) and the relation with primitives is given with its demonstration. Several technics of integrals computations and approximation are presented, as well as few examples in mechanics (time evolution), statistics (average) or continous medium (mass density) are discussed.
5. Function with several variables
Since one need to describe system which depends on many numbers (position in 3D space, time, etc ...), these function with several variables are a mandatory tool for physicists. This chapter generalizes every concept to this type of function: representation, derivation, taylor series, and integration. As a full example, the first degree polynom which minimize the $\chi^2$ for a given data sample is fully derived.
6. Vector calculus
Evaluating dynamics of fields require richer tools than derivatives. This section introduces them, up to the famous Green-Ostrogradsky theorem (link between flux and divergence) and the link between rotational and circulation. These tools in hands, Maxwell equations can be exploited such as well as any type of physics laws based on fields (ie pretty much all of them)!
7. Linear and partial differential equations
Differential equation are clearly the corner stone of the mathematical expression of physics laws. The basic mathematical theorem and methods related to differential eqautions are given, as well as key example such as conductivity model. As an example of partial differential equations, thermal diffusion and wave propagation are studied.
8. Introduction to matricial formalism
A (very) short introduction to matrices is presented in this last chapter, based on the resolution of several linea equations. The operations on matrix are given, as well as the matrix inversion using the determinant (defined as the volume generated by each vector which makes the matrix).